約4年ぶりのアイカツ8イベント! アイカツ8 2020大投票 開催中です!
アイカツ8 2020大投票が8月19日(水)からスタートしました!
アイカツ8に選ばれた8人のアイドルは、『アイカツプラネット!』のハナと9人で「公式YouTubeチャンネルで新曲が披露されるということで、みなさん自分の推しの新曲チャンスです!
8月19日(水)~9月6日(日)まで毎日投票できます。
「アイカツ!」シリーズ今でも見ている人、途中で見るのをやめてしまった人、皆さん是非投票してください!
\投票開始❣️/
— アイカツ!データカードダス公式 (@aikatsu_dcd) 2020年8月19日
アイカツ!シリーズ9年目突入&新プロジェクト発表記念
【アイカツ8 2020大投票】
投票を開始しました!
お待たせしてしまい申し訳ございません。たくさんのご参加おまちしております!https://t.co/pA67xG9yha#aikatsu #アイカツプラネット pic.twitter.com/LejLocf6dV
今回のルール
今回は各シリーズのキャラクター総勢52名から選ぶことになり、各シリーズでそれぞれ選出枠が存在します。各シリーズごとに選択肢が設けられており、1名ずつアイドルを選んでいく形となります。
- 『アイカツ!』の登場キャラ26名中、上位3名
- 『アイカツスターズ!』の登場キャラ14名中、上位2名
- 『アイカツフレンズ!』の登場キャラ11名中、上位2名
- 『アイカツオンパレード!』の登場キャラ1名中、上位1名(特殊ルール有)
『アイカツオンパレード!』だけが特殊ルールとなります。
というのも『アイカツオンパレード!』での新キャラクターは姫石らきのみとなるため、ここの1名は姫石らきと、各シリーズで選ばれなかった残りの44名で戦うことになります。
アイカツ8の歴史
アイカツ8(フォトカツ8)は2014年のデータカードダス「アイカツ!」からスタートした企画です。
人気キャラクター8名がアイカツ8としてユニットを組む形です。

最後に行われたのは、実質アイカツ8のスマホアプリゲーム「アイカツ!フォトonステージ!!」(フォトカツ)のイベント「フォトカツ8大投票」以来なので約4年ぶりとなります。
また今まで『アイカツ!』の登場キャラクターのみでしたが、今回は全シリーズ跨って実施していますのでアイカツ8史上初の試みとなります。*2
『アイカツオンパレード!』枠でのキャラクター投票の面白さ
個人的に今回面白い結果が出るなと思っています。
それは『アイカツオンパレード!』枠が姫石らきvs各シリーズで選ばれなかった残りの44名というところです。
上でも書いた通り、正直、姫石らき超不利状態なんですけど大丈夫です?なところはありますが、個々の集計結果次第で今までとはちょっと違うキャラクターがアイカツ8にくるのでは?と想像しています。
『アイカツオンパレード!』枠の集計方法が明記されていませんが、シリーズ別の選択肢で選択されたキャラクターで集計されると推測されます。
(星宮いちごを『アイカツ!』枠、『アイカツオンパレード!』枠で両方選択した場合、星宮いちごに2票ではなく、『アイカツ!』枠の星宮いちご、『アイカツオンパレード!』枠の星宮いちごにそれぞれ1票ずつになる。集計するときは、そのシリーズ単位で集計されると推測)
また、当然ですが『アイカツオンパレード!』枠のトップだった、姫石らき以外のアイドルが、『アイカツ!』『アイカツスターズ!』『アイカツフレンズ!』で選出されている場合は除外され、繰り上がっていく形になると思います。
何が言いたいかというと、『アイカツオンパレード!』枠が実質サプライズ枠となっていて、ある程度トップ層が固定されつつある「アイカツ!」シリーズにとって新しい組み合わせが誕生する可能性がある、ということです。
これは私の妄想なので順当に姫石らきが入ってくることも十分にあり得ます。
(そうなったら、らきエルザ組み合わせてきてほしいなー)
『アイカツオンパレード!』枠に誰を入れるかというのが結構重要なポイントなのではないかと思います。
特に今までのこの手のランキングでトップ10になかなかなれなかったアイドルを推している方は、各シリーズの選出枠でそのアイドルを戦わせるのではなく、『アイカツオンパレード!』枠の1枠を狙ってみるという戦略もありなのかなと思います。
ここは選択できるアイドルの数も多く投票数が散っていると推測されるので、少ない投票数でも勝ち上がれる可能性があります。
私も『アイカツスターズ!』の2枠争いで双葉アリアが来る可能性は正直かなり低いと思っているので、『アイカツオンパレード!』枠の1枠を狙う形にしています。
(『アイカツスターズ!』『アイカツオンパレード!』同名アイドルを両方投票できるので、両方投票しています)
今までの傾向から見る、アイカツ8予想
今までユーザ投票によるランキングや、ツイート数、視聴回数などを集計してきています。
そこから今回のアイカツ8でどのキャラクターが選出されるかを予想してみたいと思います。
(ただの私の妄想なので、へえくらいで読んでもらえればと思います)
私の中での今回のアイカツ8に選出されるのはこの8人だと思います。

推しの霧矢あおいも双葉アリアも入れていないのが自分でも悲しいですが……。
アイカツ!枠3枠
私は藤堂ユリカ様、星宮いちご、夏樹みくるの3人が選ばれると思います。
選出枠が3枠ありますが、実質1枠しかないシリーズです。
というのも傾向的に藤堂ユリカ様、星宮いちごはほぼ確定だと思われるためです。
他のアイドル24名で1枠を巡って戦うので、かなり厳しい戦いになると思います。
藤堂ユリカ様はどのランキングにおいても確実にトップ5圏内、今までのアイカツ8全て入っているというところから、選出確定で第何位なのかくらいが焦点だと思います。
星宮いちごも同じです。
加えて「アイカツ!」シリーズの顔でもあるため、確実に選ばれると思います。
残り1枠については、夏樹みくる、霧矢あおい、大空あかりの3人で争うのでは?と推測しています。
この3名については今までのアイカツ8で選出経験があります。
(夏樹みくる、霧矢あおい、大空あかりともに3回ずつ選出経験あり)
その中で夏樹みくるを選んだ理由としては、アイカツ8の直近のイベントであるフォトカツ8ではランクインされないものの、去年のアイドル総選挙で『アイカツ!』キャラクターで3位、『アイカツオンパレード!』の宣伝動画のランキングでも3位で、可能性があるかなと思っています。
ただ、誕生日ツイート数ではいまひとつのため、大空あかりが入る可能性もあるかなーと思っています。
(大空あかりだとあまりに順等かなみたいなところもあるので、期待もあります)
その次点で氷上スミレ、紫吹蘭、音城ノエルあたりが来る可能性があるかと思います。
音城ノエルは『アイカツオンパレード! ドリームストーリー』が直近で放送されていたので、音城ノエルの物語の集大成としてアイカツ8に入れたいと思う方もいると思いますので、3枠に来てもおかしくないかなとも思います。
アイカツスターズ!枠2枠
私は七倉小春、虹野ゆめの2人が選ばれると思います。
ここは正直七倉小春ファンがどの程度頑張るかによるかと思いますw
今までのランキング結果からみると、虹野ゆめ確定で、残りの1枠を七倉小春と桜庭ローラ、白銀リリィの3人で戦うことになるのではないかと思います。
ヴィーナスアーク所属アイドル、第25代S4は残りの1枠を争うにはいままの傾向から見ると厳しいかなと推測しています。
アイカツフレンズ!枠2枠
私は友希あいね、春風わかばの2人が選ばれると思います。
この作品で人気キャラクターココが今回いないので、推測しにくい作品になります。
春風わかばとアリシア・シャーロットのどちらかが入ってくるような気がしますが、いまいち決め手に欠けるところではあります。
コンプティークのランキングを重くみて春風わかばにしました。
(固定ファンがたくさん票を入れる可能性)
アイカツオンパレード!枠1枠
私は氷上スミレが選ばれると思います。
姫石らきvs各シリーズで選ばれなかった残りの44名です。
各シリーズで選ばれなかった残りの44名を投票する人が、単純に2番目に好きなキャラクターの中で一番好きなキャラクターにしてくるか、それが3作品のどれに偏るのかというのがポイントだと思います。
姫石らきも誕生日ツイート数が多いキャラクターなので、他のアイドルの票も散っているし順当に選ばれる可能性があると思います。
姫石らきか、氷上スミレ、紫吹蘭の3人のうちのどれかかなという想像です。
「アイカツ!」シリーズ自体の人気度からみて、単純に3番目のキャラクターを選ぶ場合『アイカツ!』のキャラクターを選ぶのではないか。
そして『アイカツ!』で次点のキャラクターのどれかがあり得るかなというのが推測理由です。
さいごに
8人という限られた枠ですので、選ばれる選ばれないはありますが、秀でている劣っているはないと思うので、好きなアイドルに投票していきましょう!自分の予想がひっくり返るように毎日霧矢あおいと双葉アリアに投票し続けます。
みんなアイカツ!どう思っているんだろう?気になったのでツイート自動分析する機能を作った
普段ツイッターでアイカツ!シリーズに関するTLを見ている人、こう思ったことがありませんか?
みんなアイカツ!シリーズの新情報やアニメを見てどういう感想を思っているだろう。
私個人としても、色々な情報を受けて皆さんがどう思っているのだろうと思っていました。
ある程度、有名な方であればリツイートされたツイート内容が流れてくると思いますが、私やその他の小さい声も含めて「今アイカツ!をどう思っているのか」を知りたいし、それを私の中に閉じるのではなく誰かに共有したい。
そんな思いから、毎日ツイッターのアイカツ!に関するツイートから、どんなキーワードがホットだったのか通知する機能を作りました。
どんな機能か
毎日、私のツイッターアカウントに
昨日はアイカツ!ついて3141人がツイートしていました。こんなワードがホットだったようです #aikatsu pic.twitter.com/styqgA0bBx
— kawase (@snofra0415) 2020年7月12日
このようなワードクラウド*1を呟いています。
(同じ言葉をつぶやいている人が多ければ、画像の文字が大きくなる図です。)
ちなみにスターライト学園の校章の形になるように作っています。
これを作った想いとよかったところ
これを作った想い
この機能を作った想いは上に書いた通りです。これを見て「アイカツ!ってみんなこう思っているんだなあ」って感じれくれればありがたいです。
自分のアイカツ!シリーズに思うことが、誰か(みんな)と同じ気持ちなのかとか、あるあるーとか、そんな気持ちの答え合わせというのもあるのかもしれないです。
よかったところ
この機能を作ってよかったところは、色々面白い結果となっている日を見ることができる点です。また私がウォッチしていないところでのコラボや、別の作品との比較でアイカツ!シリーズが語られたときにその結果を知れるというのも面白い点です。
7月は色々アイカツ!シリーズに絡んだ出来事も多く、面白い結果になっていることが多かったのですが抜粋していくつか。
昨日はアイカツ!ついて3141人がツイートしていました。こんなワードがホットだったようです #aikatsu pic.twitter.com/styqgA0bBx
— kawase (@snofra0415) 2020年7月12日
まず、先ほど紹介したツイートは『アイカツオンパレード!ドリームストーリー』5話6話の公開日のツイートをまとめたものになります。
音城ノエル主人公で大空あかりとの絡みが強かったので、みんなこのふたりのことを呟いているんだなーって分かります。
昨日のアイカツ!界隈はこんなワードがホットだったようです #aikatsu pic.twitter.com/dflWcpwsue
— kawase (@snofra0415) 2020年7月4日
この日は『アイドルマスター ミリオンライブ!』のテレビアニメ化が発表されて、脚本が『アイカツ!』をご担当された加藤陽一さんだと分かったときのちょっとした祭りの状況です。
『アイドルマスター ミリオンライブ!』、TVアニメーションプロジェクトの始動が発表となりました。シリーズ構成・脚本を担当させていただきます。よろしくお願いいたします!
— 加藤 陽一 Yoichi Kato (@yoichi_kato) 2020年7月4日
信頼や期待というワードがあるので、かなりポジティブな感想を思っているんだなーというのを強く思いました。
このような情報を得られるのが作ってよかったなあって思います。
昨日はアイカツ!ついて2419人がツイートしていました。こんなワードがホットだったようです #aikatsu pic.twitter.com/QmCxBJ7QP1
— kawase (@snofra0415) 2020年7月14日
この日は『ラブライブ!スーパースター!!』の情報が解禁された日で、アイカツ!とは直接的に関係はありませんが、キャラクターデザインが『アイカツ!』っぽいというつぶやきをした人が多かった感じですね。
昨日はアイカツ!ついて2103人がツイートしていました。こんなワードがホットだったようです #aikatsu pic.twitter.com/lspnBhJfwJ
— kawase (@snofra0415) 2020年7月19日
DCD『アイカツオンパレード!』の大規模障害発生時のツイートになります。
やはり皆さんオンラインでプレイができなくなったので、つぶやいている感じですね。
好き!って気持ち
この機能を作ってすごく目にするのが、「好き」ってワードです。毎日たくさんツイートされている言葉のひとつです(もうひとつは「アイカツおじさん」)。
加えてネガティブなワードが少ないなというのも思ったことです。
ネガティブなワードが今回収集しているツイートのキーワードに含まれてないためというのもあるかもしれませんが、ほぼ出てきません。
(私の方で意図的に除外したりは行っていません)
アイカツ!というコンテンツがかなり愛されているんだなーというのがとてもよくわかるし、こういうツイートがあるうちはコンテンツも安泰なのかもなというのが素直に思うことです。
また、「アイドルマスター」や「プリキュア」、「プリパラ」、「プリチャン」などのワードも毎日出ていますので、どうやらアイカツ!は他の作品と比較して語られているようです。
今後やりたいこと
毎日、ツイート数やツイートユーザ数も集計しているので、これは別途まとめた記事を作って定期的にお見せできればいいなあと思います。技術的な当機能
以下技術的な要素を多く含みます。
機能について
今回はAWS Lambdaを組み合わせたサーバーレスな機能を作成しました。今回の構成は以下となります。
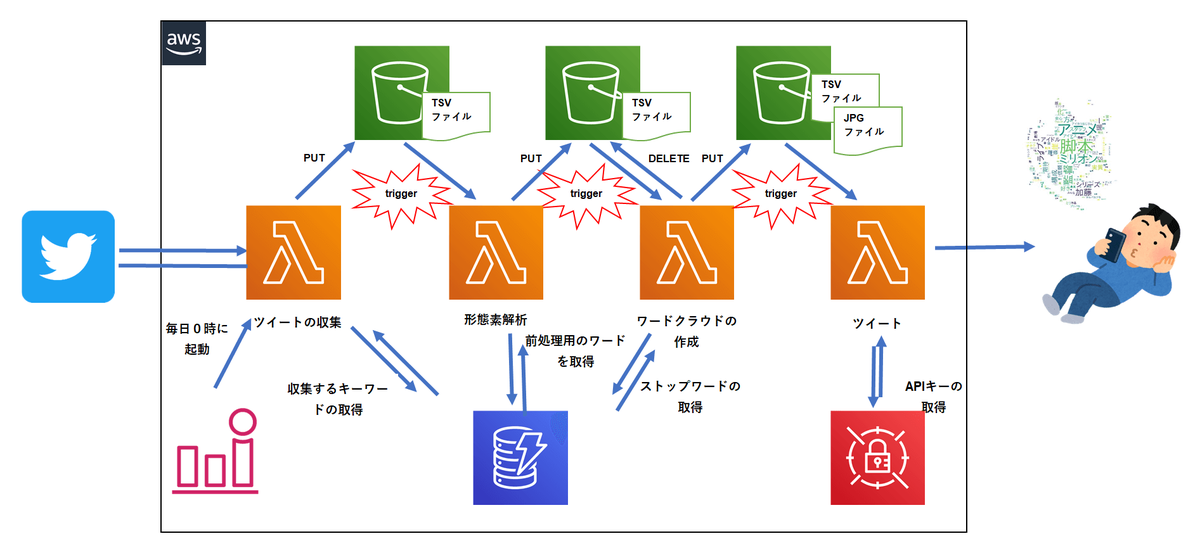
処理としては
1.毎日0時にCloudWatch アラームが発火してAWS Lambdaのツイート収集機能が実行、ツイート内容と、ツイートユーザ、ツイート数をAmazon S3にPUT。
2.PUTをトリガーにMecabでの形態素解析を実行、その結果をAmazon S3にPUT。
3.PUTをトリガーにワードクラウドを作成し、作成した画像をAmazon S3にPUTして、形態素解析の結果を削除
4.PUTをトリガーにツイートをPostする。
各機能を分割しているのは、そもそもの問題としてAWS lambdaのデプロイパッケージの上限である250MB制限に引っかかってしまう問題。
あとは、リファクタリングをする際に疎結合にすることでメンテナンスの容易さを担保するためです。
docs.aws.amazon.com
AWS Lambdaだけでなく、パラメータなどもすべて他サービスによせていってます。
私しかメンテナンスしないので、コードにAPIキーとかハードコーディングでもよかったですが拡張性の担保、メンテナンス性の容易さから極力他サービスによせています。
AWS lambdaの制限であるデプロイパッケージの上限250MBによって、形態素解析する際の辞書でNEologdが使用できないのがちょっと痛いです。
うまく形態素解析ができず、変なワードで切り取られてたりしてしまうのがいくつかありました。
縮小版 NEologd辞書を使用する等することで使用できるっぽいですが、見送っています。
理由としては今回はNEologdよりもアイカツ!シリーズに関するワードを登録したユーザ辞書を拡充するほうがよりよいだろうという理由です。
ユーザ辞書には以下のような情報が格納されています。
- キャラクター名や「スターライト学園」などの舞台、それぞれのアイドルが着るドレスのブランド名、「芸能人はカードが命」などの有名なセリフなど劇中で登場するワード
- 168曲分の曲名
- コーデ名(カードテキスト)や「フィーバータイム」など「DCDアイカツ!」~「DCDアイカツオンパレード!」での用語やコーデ名
- 「せなあか」のようなカップリングや「なまくら」などファン間での呼称
- 声優や歌唱担当などのスタッフ・キャスト情報
- その他、「アイカツ!」シリーズとセットで話されている「電音部」や「バトスピ」などのワード
これが一番作るの面倒くさかったですね。
作成に当たっての思い
ひとりのアイカツおじさんとしての思いは上に書いた通りです。技術者としての思いとしては、今回使用している技術はそれぞれ単体でアドホック的に使用している側面が強く、組み合わせた機能を作りたいなという点、
極力お金は使いたくなかったので、サーバーを立てるよりはサーバーレスで実施したいという気持ちからです。
業務でサーバレス環境構築しているというのもあります。
作成期間は1か月程度で毎日2時間程度構築していった形となります。
特にアーキ設計はしていないので、なんとなくLambdaひとつずつ作成して後からリファクタリングで別サービスと連携していった形となります。
課題
この機能まだまだ課題がたくさんあるので修正したいなという思いが強いです。主に以下2点で、ともにツイートの収集部の不具合になるものです。
・障害発生時のリカバリ
・ツイート収集のライブラリ不具合
ツイートの収集部は、twitterscraperというライブラリを使用しているのですが、twitterサービスに寄り掛かったライブラリのため、twitter側のアップデートによって使用できないことがあるのが問題です。
こんな感じになる。
昨日はアイカツ!ついて0人がツイートしていました。こんなワードがホットだったようです #aikatsu pic.twitter.com/ZDjoUdv3hN
— kawase (@snofra0415) 2020年8月12日
この機能は毎日ツイート情報を取ってくるもので、ツイート数も1万程度しか存在していないので、tiwtter APIに倒してしまってもよいのかなと思います。
(このライブラリもグレーな要素が強いので、ちゃんとしたものに変えたほうが良いのではというのもあります)
また、どういう理由かは分からないのですが、まれにツイート収集が15分で終わらないケースがあります。
その場合、AWS Lambdaの仕様上処理が終わってしまうので結果が中途半端になるという問題が発生、再実行で解消するのですが、再実行するのにわざわざAWS Lambdaまで行かなければならないので、LINEとかからキックできるようにしたい。
次は実写×アニメ!新番組『アイカツプラネット!』の発表で見えてきたもの
アイカツ!シリーズ最新作『アイカツプラネット!』が2020年8月10日のBANDAI × BN Pictures Festival (BBフェス)で発表されました!
【BBフェス】BANDAI × BN Pictures Festival 『アイカツプラネット!』パート
発表された内容と、それらにかかわる数字について書いていきます。
2021年1月より放送開始『アイカツプラネット!』
上の画像を見ても分かると思いますが、今度は実写パートとアニメ(3DCG)パートがあるようです。
発表開始時のPVからあれアニメキャラクターではなく、人が出てきた?ってなりましたが、まさかドラマパートがあるとは……。
想像の斜め上の発表で正直驚きました。
発表時の反応もそうでしたが、アニメじゃなくてドラマなの?という動揺や、「アイカツ!」ではない、微妙という雰囲気があるように見えました。
これも予想外すぎる発表だったというのも関係あるのかなと思います。
アニメについての詳細の情報は、今回解禁された時点ではあまり公開されておらず、概ね以下の情報のみとなります。
本コンテンツの主人公・音羽舞桜は,ある日突然姿を消した陽 明咲の代わりに,憧れの世界「アイカツプラネット!」のトップアイドル・ハナとして活動することになる。ハナになった舞桜は,「スイング」と呼ばれるアイテムに宿る「ドレシア」の力でドレスアップし,ライバル達との熱いパフォーマンスバトルを繰り広げることに……というのが本作のストーリーである。
アイカツ!シリーズ新プロジェクト「アイカツプラネット!」が発表。実写・アニメ・3DCGをミックスした新しい表現に挑戦する意欲作
後述しますが、「「スイング」と呼ばれるアイテム」が今まで言うところのアイカツ!カードになります。
「アイテムに宿る「ドレシア」の力」というのが、アイカツ!シリーズでいうところのコーデですかね?
ドレシアにはタイプがあるらしく、フェアリーやジュエルなどがあるらしいです。
この辺はもう少し詳細な情報がないとよくわからないですね。
スタッフ情報
スタッフ情報については更新サイトにも記載がありますが、木村隆一さんが総監督・監督なのが一番のポイントですね。
『アイカツ!』で監督をやられていたいわばアイカツ!シリーズを創り上げた方のひとりでもあるので、この大きく変わったアイカツ!を創り上げるのに適任という感じになったんでしょうか。
シリーズ構成の千葉美鈴さんは『アイカツスターズ』でアイカツ!シリーズにかかわった方で「妖精アイドル 双葉アリア♪」という(個人的な)神回を作っているので楽しみです。
キャラクターデザインの宮谷里沙さんはアイカツ!シリーズといえばって方ですね。
アイカツ!の大きな変更について思ったこと
ドラマパートがあるという発表で、上でも書いた通り微妙な雰囲気が思いますが、アイカツ!シリーズのコンテンツの存続という観点であれば正直このくらい変わらないとダメというのは正直あります。
アイカツ!シリーズの売上的にもこのまま小さいバージョンアップを繰り返していても、現在のビジネスモデル的にもアイカツ!というコンテンツに勝機がない可能性が高いかなと思っていました。
(アイカツフレンズ!ではビジネスモデルをアイドルマスターのような声優を使ったビジネスによせようとしましたが、今回それを止めたというのがはっきり見えた形ですね)
アイカツ!シリーズの売上情報については以下を見ていただければと思います。
snofra.hatenablog.com
また昨今のガールズ戦士シリーズや、演者の方によるユニットGirls2が現在アイカツ!のターゲット層で人気という背景もあると思います。
小中高生向けNHKの番組『沼にはまって聞いてみたでも』特集が組まれているくらいなので、人気度は高いと思います。
ガールズ戦士シリーズは、EXILEなどが所属している株式会社LDH JAPANに所属している方が出演していますが、『アイカツプラネット!』では株式会社スターダストプロモーションに所属している方がメインキャラクターを演じるという感じです。
株式会社スターダストプロモーション版、ガールズ戦士シリーズという見方もできるかと思います。
個人的には今までずっとアイカツ!シリーズの傍らにいた株式会社ホリプロとの連携もなくしたのは思い切ったなと思いました。
株式会社ホリプロでは、今までアイドルグループがいなかったということもあってノウハウ不足を問題視されたのかもしれません。
DCD『アイカツプラネット!』は今冬稼働予定
アニメの情報に加え数分ではありましたが、データカードダス『アイカツプラネット!』についても発表されました。
データカードダス アイカツプラネット! プロモーションビデオ
ぱっと見ても今までの筐体とかなり違いますね。
今回発表されて分かったこととしては、
- アイカツ!カードから「スイング」と呼ばれる正方形型のアイテムに変更
- ボタンが廃止され、スクリーンにタッチしてゲームをするように変更
紹介された時点ではゲームをプレイしていないので、具体的にどういう感じに変わったのかは判断できない状態です。
またスイングについても、カードイラスト側のみだったため裏面がどうなっているのかもわかりませんでした。
過去シリーズの互換性についても特別言及はされませんでした。
ただ筐体を見て推測できることとしては、
- スイングの読み込みは『プリパラ』、『プリチャン』の方式に近くなっている(筐体の中に入れる仕組み)になっているっぽい?
- 筐体の右端に2次元バーコードの読み取りがありそうに見えるので、過去カードはそこでスキャンする?
こんな感じかなーと思います。
スイングは持っている感じ今までのアイカツカードとは材質が変わっているのかなと思いました。
ペラペラ感があまりないよう見えました。

引用:アイカツ!シリーズ新プロジェクト「アイカツプラネット!」が発表。実写・アニメ・3DCGをミックスした新しい表現に挑戦する意欲作
上のイメージ図を見る限りは、バインダーに入れて保存するコレクター的な要素に加えて、専用のホルダーに入れて見せるアクセサリーのような要素を含んでいるものと思います。
(グッズ展開としても専用ホルダーや、専用ホルダーに入った限定スイングの発売なども考えられているのかなと思います)
今までもアイカツカードを入れるバインダーも持ち運びやデザイン性を考慮して展開してきているので、デザイン性に特化してくるというのはなんとなくわかりますね。
(きっと各キャラクターイメージのバインダーも出るだろうなー)
現在稼働中のDCD『アイカツオンパレード!』は10月頃に現行の筐体での最終弾が出るのではないかと思います。
今回の発表をめぐる数字
Twitterのツイートツイート情報
まず、Twitterでのツイートについてですが、アイカツ!シリーズ自体の大きなアップデートということもあり、観測を始めて一番ツイートされていました。
発表時の8月10日はツイート数が13,846ツイート、ツイートユーザ数が8,494ユーザでした。
発表翌日の8月11日はツイート数が9,666ツイート、ツイートユーザ数が6,524ユーザでした。
これはツイートに「アイカツ」や「#aikatsu」などがついた状態でのツイート数ですので、ついていないツイートを含めるとそれ以上のツイートがされていると思われます。
『アイカツオンパレード!ドリームストーリー』の最終回がツイート数10,011ツイート、ツイートユーザ数が3,141ユーザでしたので、これから比べてもかなりの人が『アイカツプラネット!』の発表を見ていたということが分かります。
(アイカツ!シリーズの新情報がないときは大体ツイート数は2,000くらい)
8月10日でひとりの人がツイートしていた数は約1.63で、大体ひとり2回くらいはツイートしている感じですね。
ただ今回は実況系と違う性質のものになるため、明示的にアイカツと書かない人もいると思うので、実際はもう少し新情報についてツイートしていると思います。
具体的なツイートされた文章の傾向ですが、やっぱりというか実写が一番ツイートされていますね。
昨日はアイカツ!ついて8494人がツイートしていました。こんなワードがホットだったようです #aikatsu pic.twitter.com/hbCcEsQrqa
— kawase (@snofra0415) 2020年8月10日
翌日についても同様ですね。
昨日はアイカツ!ついて6524人がツイートしていました。こんなワードがホットだったようです #aikatsu pic.twitter.com/N5nzIWVhLV
— kawase (@snofra0415) 2020年8月11日
やっぱりみんな実写になったことについて何らかな感情を持っていることが分かりました。
Youtubeチャンネル「アイカツプラネット!ステーション」の動画再生数
8月13日現在で3つの動画がアップロードされています(8月10日20時にアップロードされたもの)
【BBフェス】BANDAI × BN Pictures Festival 『アイカツプラネット!』パート
データカードダス アイカツプラネット! プロモーションビデオ
【アイカツプラネット!】はじめまして!伊達花彩です!【音羽舞桜/ハナ役】
それぞれの動画の0時時点の再生回数をまとめたものがこの表となります。
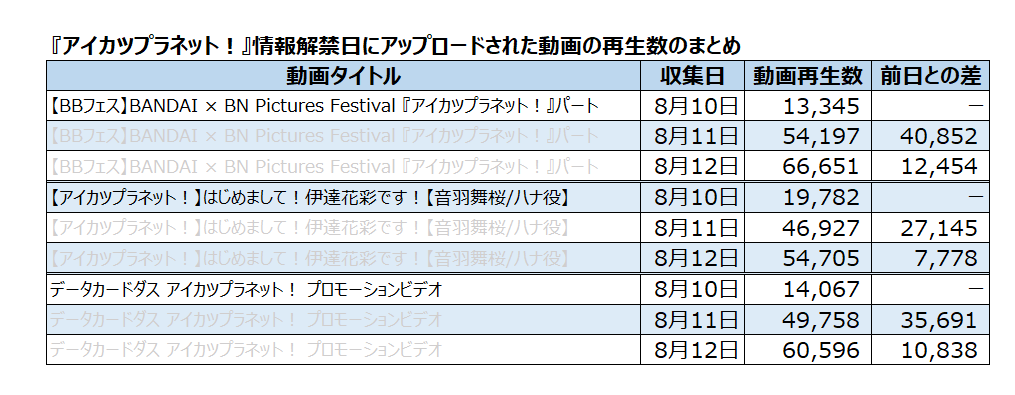
この3つの動画の中で伊達花彩さんの紹介動画が上がっているのが、BBフェスでアイカツ!新シリーズの情報よりもアイドルたちの紹介に終始したという状況にも関連するのかなーと思いました。
『アイカツプラネット』自体の進捗状況は窺い知れませんが、各アイドルたちを知ってほしいという気持ちのほうが強いのかもしれません。
私含めて実写×アニメで動揺している状態だったので、アイドル紹介よりもそういう世界観なのかとか、スタッフの方にもご登壇いただいたほうが良かったのかなというのはあったかなと思います。
さいごに
今回の発表は、まだまだ分からないことがたくさんあるなという感想でした。またドラマパートがあるという要素から、おそらく以前あった歌唱担当全員卒業というもの以上に波紋があるだろうと思っています。
その結果としてアイカツ!シリーズから距離を置いてしまう方も少なくないのかなという感想でした。
そればっかりは仕方ないと思いますし、公式側もそれは覚悟していることだと思います。
個人的にはすごく残念な気がします。
正直あまりにも突拍子もない発表だったので不安がないとは言えません。
ただあまりにも情報が少なすぎるので、今離れるのではなく、もう少し待ってみて「アイカツ!」らしさがあるのかどうかもう少し見定める時間を設けてほしいという気持ちも少なからずあります。
『アイカツプラネット!』これからも注視していきたいと思います。
『アイカツオンパレード! ドリームストーリー』はみんな見てる?再生回数や実況ツイートから見えること(3話まで)
『アイカツオンパレード! ドリームストーリー』がWEBアニメとして3月28日からバンダイチャンネルで配信スタートしています。
現在は3話まで公開されています。
今追いかけても1時間かからないので、まだ見たことのない方は是非見てほしいです。
主人公はドリームアカデミーの音城セイラの妹、音城ノエルです。
『アイカツ!』は見ていたけど、主人公が大空あかりになってみてないなあって人や『アイカツスターズ!』から見ていないなって人でも大丈夫です。
そんな『アイカツオンパレード! ドリームストーリー』に関する数字について書いていきたいと思います。
条件
分析にあたり以下を条件としています。- 『アイカツオンパレード! ドリームストーリー』の配信先は「あにてれ」などありますが、今回はYouTubeを対象としています。
- YouTubeの再生回数は自前のツールで毎日0時に取得しています。
- ツイッターのツイートについても自前のツールで取得しています。(検索条件:#aikatsu、#アイカツオンパレード、#aikatsuonparade)
次の配信までの日数が少しずつ伸びていっている
まずは動画の配信日時・動画時間からみえることについてです。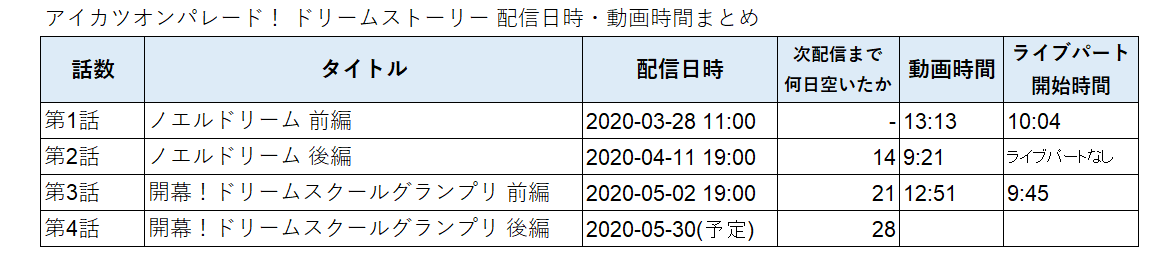
どうやら次の配信まで1話進むごとに1週伸びていること分かります。
1話から2話までは2週間でしたが、3話から4話は4週間空いています。
どんどん配信日が伸びてしまっている背景は読み取ることはできませんが、コロナウィルス下でのアニメ制作がストップしてしまっていることも少ならからず影響しているかと思います。
1ヶ月2話くらいのペースのため、仮に秋アニメで「アイカツ!」シリーズの新シリーズが始まる場合、ドリームストーリーは全10話程度になるものと推測されます。
ストーリー展開的にドリームアカデミー以外の学校は各1話ずつくらいで学校代表者1名が決まって、決勝戦、エピローグで10話くらいなのかなと思います。
また、1話につき大体10分~15分いかない程度で、ライブパートを除外すると大体各話9分程度のアニメということが分かります。
YouTuberの動画の時間に合わせて15分前後としているのでしょうか。ここのねらいについてもよくわからないです。
3話までの動画の平均時間は約11分なので、仮に10話までやったとしても110分、2時間もかからないので追いかけてみるにも優しいアニメになりそうです。
動画の再生回数と実況ツイートから見えること
次に動画の再生回数と、実況ツイート数になります。
これをみるとどのくらいの人が動画を見ているのかがなんとなく見えます。
ただしWEBアニメという特性上、通常のテレビ放送よりもリアルタイム性は薄れてしまっているとは思います。
あくまで目安としてという形となりますが、公開されてから1時間での実況ツイートをまとめています。
これを見てまず分かるのは、再生回数が話数が進むと落ちているというところになります。
これは1話から2話を見ると顕著に出ていますね。
1話は初日で55,000くらいの再生回数ですが、2話は15,000くらいまで落ちています。
また、実況ユーザ数も700くらいから340まで落ちてしまっているので、おそらく1話で切ってしまった人(脱落者)が5割程度いるだろうと推測できます。
1話は『アイカツオンパレード!』の最終回も同日で、1話の配信が最終回直後であったということもあり、ユーザーが流れていったためご祝儀的に再生数が増えているのだと思います。
一方で必ずしも話数が進むと脱落者が増えているというわけでもないようです。
2話から3話をみると、再生回数は減っているが、実況ツイートユーザ数は(誤差レベルですが)伸びています。
キャンペーンも実施していたので、この施策の成果が出ている可能性が考えられますね。
公式側もある程度の脱落者が出ると見越して、脱落者を減らそうとしている意図が見えます。
【WEBアニメを見てみんなでアイカツ!キャンペーン】本日公開!19時からアイチューブでプレミア公開♪みんなで一緒に楽しもう☆# 付きツイートをすると抽選で豪華景品が当たるキャンペーンは5月3日まで開催してるよ☆https://t.co/8kEqlfJwC6#5月2日19時アイカツWEBアニメ大視聴会 #aikatsu pic.twitter.com/ncHl3nKEwS
— アイカツオンパレード!アニメ公式 (@aikatsu_anime) 2020年5月2日
4話は、3話から4週間後の配信で正直忘れている人も多いと思いますので、キャンペーンをどんどん打っていってほしいところです。
また、2話から3話の再生回数と実況ツイートユーザ数の関係から言えることがもうひとつあって、それは同じ話を周回していない可能性が考えられるという点です。
ツイートユーザ数が伸びている場合、再生回数も比例するのかなと思っていましたが、結果としてそうではなかったので、ひとりが見る回数が減った可能性があると思います。
さいごに
まだグラフにプロットするほどの数も出そろっていないため、数字の一覧から想像できることを書きました。もう少しデータがそろった時点で自覚的な情報も増やしていけたらと思います。
『アイカツオンパレード!』の売上はどうだったのか?決算短信から確認してみる
2019年の通期決算短信が出ましたので、バンダイナムコの決算短信から『アイカツ!オンパレード』の結果について記載していきたいと思います。
まとめる期間は2020年3月期 通期までの決算短信です。
具体的な期間としては2013年1月から2020年3月までとなります。
※途中で決算短信上掲載されていない2018年3月期 第1四半期から第3四半期は、翌年の情報から確認しています。
2018年の結果については前回書いた内容を見ていただければと思います。
なお今回についても「プリキュアの数字ブログ」を思いっきり真似しています。
2019年通期の売上高結果
「アイカツ!」シリーズの2019年通期(2019年4月~2020年3月)の売上高は32億円となります。前年2018年通期の売上高は30億円のため、前年比約107%成長のため、前年よりも若干ですが売上が伸びたということになります。
トイホビーの売上は16億年、前年は19億円のため、前年比84%成長です。
全体の売上は伸びていますがトイホビーの売上は成長率が低いのが分かります。
メインコンテンツであるデータカードダスや「アイカツ!スタイル」のようなアパレルの方向性から、ライブによる収益にシフトしている傾向が読めるように思えます。
※トイホビーの定義は(玩具、カプセルトイ、カード、菓子・食品、アパレル、生活用品、プラモデル、景品、文具)です。
各年度別売上高

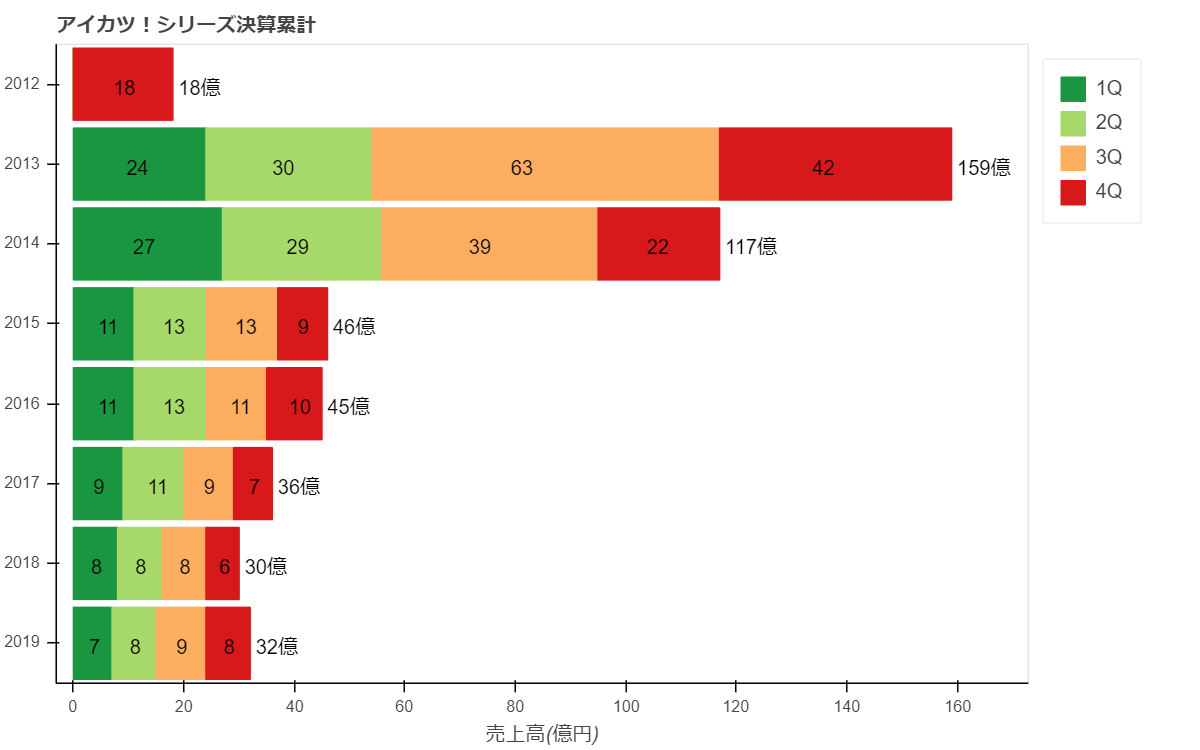
※「アイカツ!」シリーズはCDやBlu-ray Disc等の映像音楽についてもバンダイナムコグループのため、決算短信の売上高の対象となっています。
シリーズ別売上高
※バンダイナムコ公式の集計ではありません。※シリーズで開始時期が異なるので、四半期単位でまとめています。
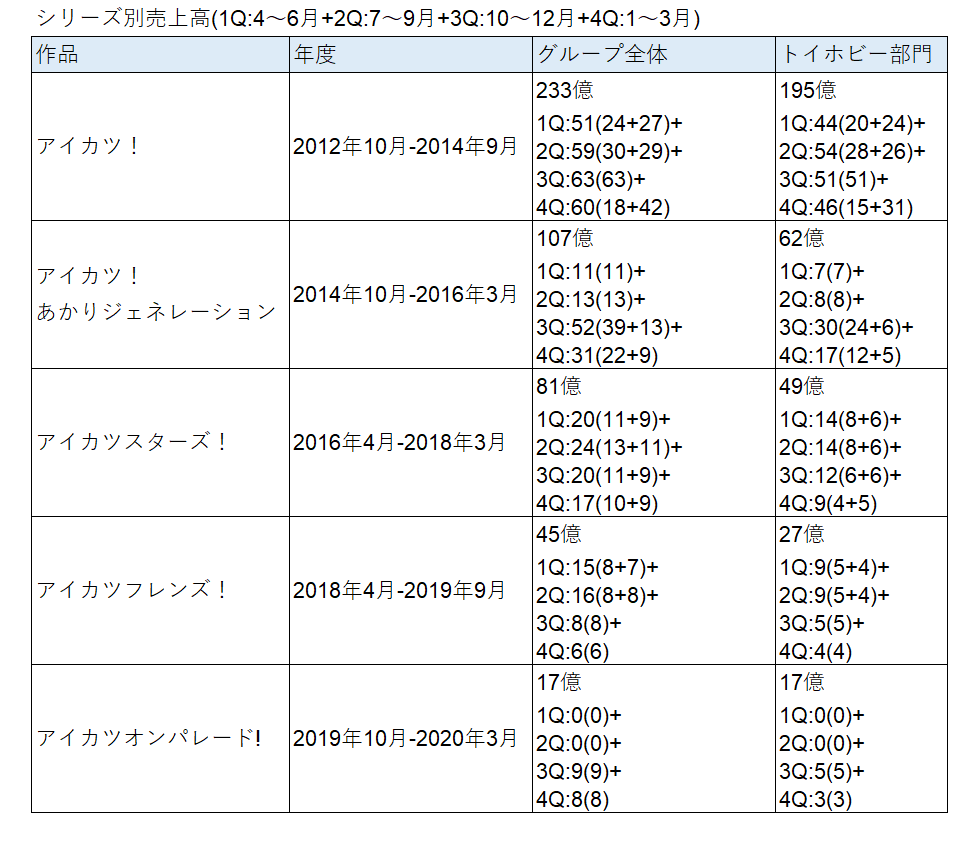
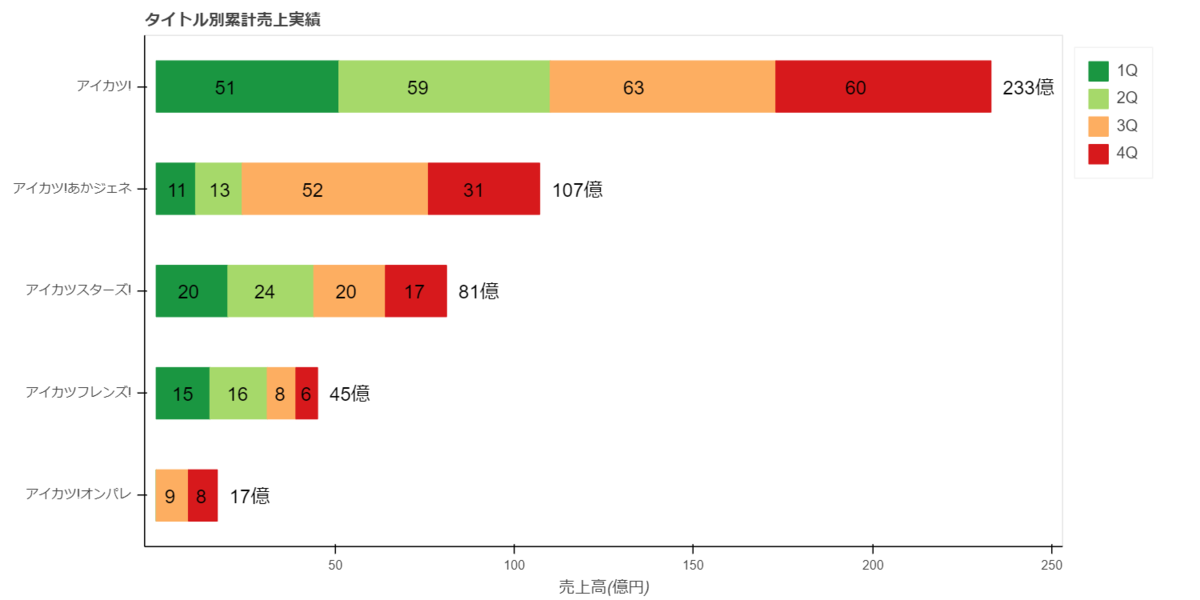
売上実績と通期計画の差
1年の計画に対して売上がどうだったかを見てみます。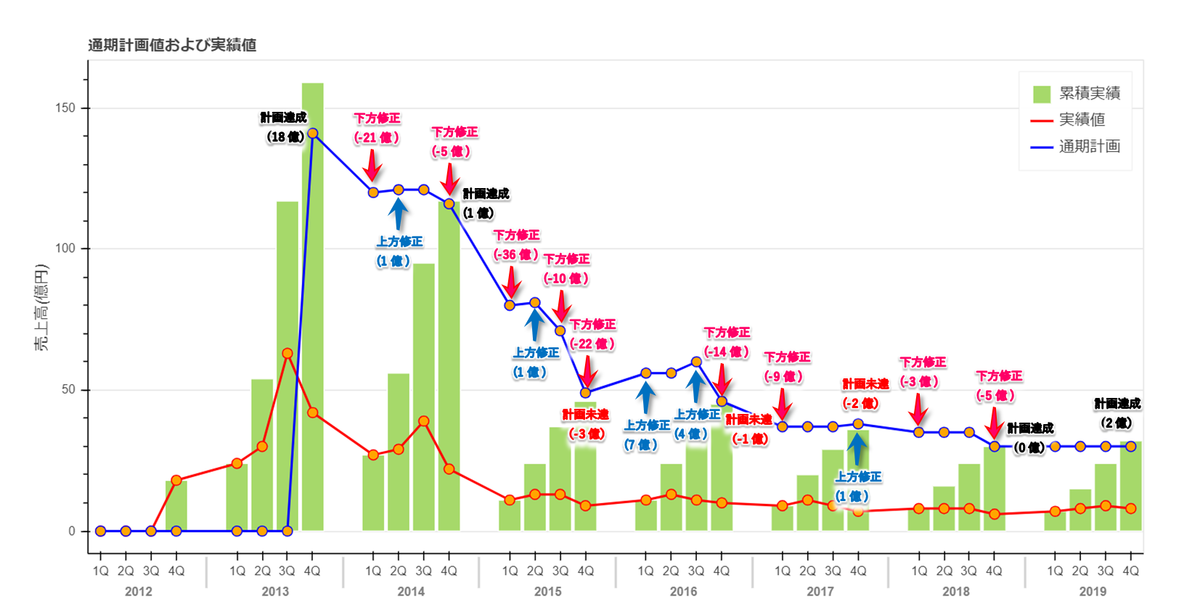
この図は1年間の計画(通期計画)に対して、売上高(実績値)が達成できたのかどうかを表しています。
赤線は各四半期ごとの売上高、緑色の棒グラフは累計値です。
通期計画が下方・上昇修正しているのは売上高の好調不調により調整されるものです。
2019年の計画値30億円に対して、結果は32億円でしたので計画は達成しました。
2018年の最終的な計画値も30億円でしたので、2019年に実施した施策が成功していると考えてもよいと思います。
この図を見ると分かるのですが、次の2020年の計画値が存在しません。
理由はコロナウィルスによるものです。
バンダイナムコ全体の業績予報についてもコロナウィルス感染拡大の影響が多岐にわたることから算定が困難ということで未定になっています。
2019年のアイカツ!シリーズはどうだったのか
2019年度~2020年度は「アイカツ!」シリーズにとっては大きな転換点といえる年だと思います。- 今までのキャラクターが登場する新シリーズ『アイカツオンパレード!』
- 「『アイカツフレンズ!』BEST FRIENDS! スペシャルLIVE ~Thanks⇄OK~」や「バンダイナムコエンターテインメントフェスティバル」、「アイカツオンパレード!ライブツアー」など大きなライブ回数
- バトルスピリッツなど異なるコンテンツとのコラボレーション
- アニメの配信媒体の変更
- (今後)データカードダス新シリーズ
これらの施策によって売上が良くなっていったのだと思います。
ライブに関連しては、今も過去の施策の失敗に絶望して去って行った方の声も聞きますが、ライブ収益によってコンテンツを支える方針は、トイホビーが成長率が落ちているが、全体の売上が伸びたという点からも成功していると言っていいと思います。
おそらく今後についてもこの方針は継続していくと思います。
コロナウィルス下でのアイカツ!シリーズへのダメージ
他のコンテンツも同じ状況ではありますが、「アイカツ!」シリーズへのダメージはかなり大きなものとなります。そのひとつにライブ・コンサートの中止があります。
ライブ・コンサートの中止により、第4四半期連結会計期間(1月~3月)での売上に影響があったと推測されます。
開催された場合、グッズ販売などでもう少し売上があった可能性があります。
また、ゲームセンターやアイカツ!スタイル(アパレルショップ)の営業自粛による影響により、データカードダスやアパレルの売上にも影響があったかと思います。
【店休のお知らせ】
— アイカツスタイル公式 (@aikatsu_style) 2020年5月6日
この度の緊急事態宣言延長に伴い、5月7日(木)以降も当面の間、臨時休業いたします。
お客様にはご迷惑をおかけ致しますが、ご理解宜しくお願い致します。
⭐️WEBSHOPhttps://t.co/zxJmTKp1pY#aikatsu #アイカツオンパレード pic.twitter.com/Oc99AiKhtO
今後の「アイカツ!」シリーズの商品展開として予定していた「アイカツ!シリーズ新プロジェクト」についても発表が延期になりました。
2020年6月に予定していた「アイカツ!シリーズ新プロジェクト」の発表につきまして、新型コロナウイルスの感染拡大の影響により、安全に皆様に情報をお届けするため、発表を延期させていただくこととなりました。発表日時、発表方法などの詳細情報については後日公開致します。#aikatsu
— アイカツオンパレード!アニメ公式 (@aikatsu_anime) 2020年5月14日
また、現在は特別アナウンスされいない状態ですが、データカードダス新弾のリリース日も延期になっていくと思います。
「アイカツ!」シリーズの現在の主な売上は、データカードダス、ライブ収入、アパレルの3点だと思います。
コロナウィルスがどの程度続くかは判断できないですが、2020年中続くようであれば2020年度の「アイカツ!」シリーズの売上はかなり厳しいものになると推測されます。
星宮いちごの誕生日はどれだけ祝福されているのか?ハッシュタグから見えること
去る3月15日は星宮いちごちゃんの誕生日でした。
お誕生日おめでとう!
私のツイッターアカウントでも「アイカツ!」シリーズが好きな方をフォローしているのですが、今年は何となく「星宮いちごHBD!」みたいな投稿を見ることが多かったように思えます。
#星宮いちご生誕祭2020 #星宮いちご生誕祭 みなさんスゴい。ありがとうございます。大変な時期にもお祝いしてもらえてるのを見て、企画していた震災前後の頃を思い出しました。1期再放送も最後までぜひ。最終回の音楽のことも載ってる記事、改めて読んで面白かったhttps://t.co/dOy4r1JRtT #aikatsu
— 加藤 陽一 Yoichi Kato (@yoichi_kato) 2020年3月14日
とツイートしているので、どうやら私の観測だけではないようです。
ちょっと気になったので、星宮いちご誕生日お祝いツイートについて調査してみます。
ルール
調査にあたり以下をルールにしています。- twitterのハッシュタグ「#星宮いちご生誕祭」か「#星宮いちご生誕祭yyyy」(yyyyはその年、今年であれば2020が入ります)を調査対象とします。
- 上のハッシュタグを両方つけている場合はひとつのツイートとして集計します。
- 同一ユーザの複数ツイートもハッシュタグが付いていれば集計対象ですが、リツイートは集計から除外しています。
- 調査期間については星宮いちご誕生日3月15日の前後1週間を集計します(3月8日~3月22日)。※絵師さんで遅刻される方の救済
ツイート数から分かること
2020年までのツイート数と前年比は以下になります。
ぱっと見ただけでも2019年、2020年のツイート数すごいですね。
かなりツイート数が伸びた2019年
2019年は、2018年から約160%伸びているので一体何が起こったんだ?というようなレベルです。正直ここについては要因がよくわからないです。
アニメでは『アイカツフレンズ!』放送中なので、アニメで登場してきたということではありません。
また『DCDアイカツフレンズ!』も第6弾稼働中ですが、特に星宮いちごのイベントがあったわけでもないと思います。
2020年も順調にツイート数が伸びています
今年、2020年は2019年から約120%ツイート数が伸びていました。2019年よりは伸びていませんが、2019年から順調にツイート数が伸びてきているのは『アイカツオンパレード!』で「アイカツ!」シリーズを見始めた人、戻ってきた人が多かったの可能性が高いですね。
この点のみ見る限りは『アイカツオンパレード!』は正解だったのかな?と思います。
前年度比は2015年が圧倒的
前年からの伸びという点では、2015年が圧倒的です。前年度比270%は、おそらく今後も超えることはないと思います。
2015年3月15日付近は第124話「クイーンの花」が放送された時期になります。
主人公が星宮いちごから大空あかりに代わってから22話後ですね。
以下で書いている「アイカツ!」シリーズのピークは2013年~2014年説からすこし外れているのが面白いところだなと思います。
snofra.hatenablog.com
2013年~2014年の集計数が取れなかったのは、もともとハッシュタグ自体がなかったというのが考えられます。
『アイカツスターズ!』時期に苦戦
順調ではない時期もあり、2017年~2018年の伸びはよくなく、2017年は前年よりもツイート数が減っています。前年度比は-2%。2017年~2018年は『アイカツスターズ!』放送時期になります。
『アイカツ!』というタイトルも変わり、舞台も変更されたので星宮いちごファンが離れていってしまったと考えてよいと思います。
全体を見ても圧倒的に祝福されている
星宮いちごお誕生日おめでとうツイート数は全体の何%くらいなのかという点を見てみたいと思います。wikipedia等で誕生日が判明しているキャラクターは62キャラクターです。

単純にツイート数で集計してしまうと登場年が古ければ古いほど有利になってしまうので、各キャラクターのツイート数の平均値で計算しています。
全62キャラクターの平均値の合計は約13586ツイートです。
その中で星宮いちごの平均ツイートは約1008ツイートで全体の7.4%でした。
2位の霧矢あおいが4.5%、平均ツイート数が613ツイートなので380ツイート差をつけての2位になります。
380ツイートというのはあくまで平均値なので、1位になろうとするには毎年星宮いちごのツイート数を越えることが前提になるので、この差が埋まる可能性はないと思います。
星宮いちごの今年結構お誕生日おめでとうツイートされているなと最初に書きましたが、そうではなく毎年ツイートされているといったほうが良いかと思います。
みんなから祝福されている
最後にツイートユーザ別で見てみたいと思います。ツイート数だけだと、最悪ひとりが2000ツイートしている可能性があります。
それはみんなに祝われているのか?という疑問があるので、どのくらいの人に祝われているのかも見てみたいと思います。
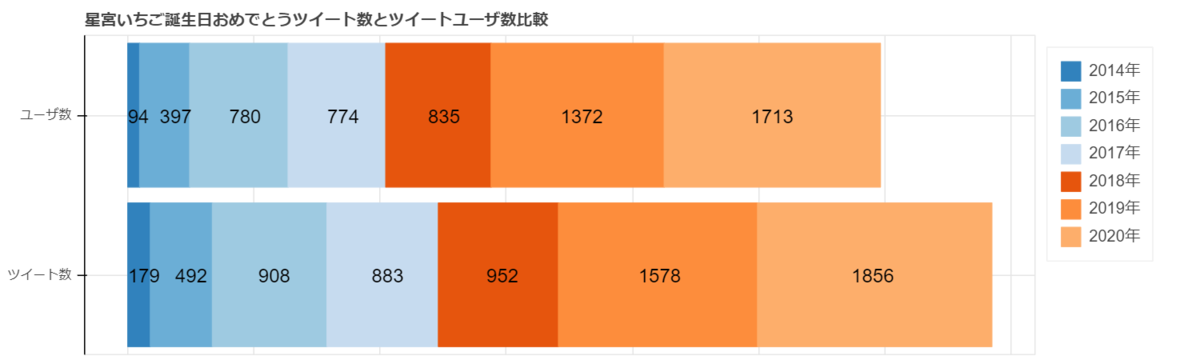
2014年のツイート数とツイートユーザ数がかなりずれていることが分かります。
ひとりあたりのツイート数を見るともっとよくわかります。
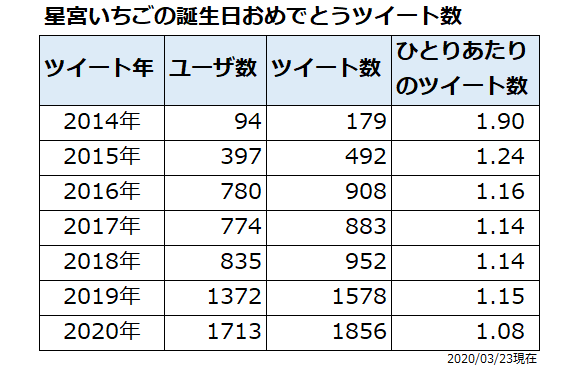
2014年はひとりあたりのツイート数は1.9ですが、2020年は1.1なので、2020年はひとりあたり1ツイートしていますが、2014年は2ツイートしていますね。
ここから見るに2014年はまだ、このハッシュタグができたばかりで広める目的もあったのだろうと思いますが、2020年は完全に浸透したという感じなのではと思います。
それにしても1863人に祝福されるというのは、さすがアイドルって感じですね。
最後に
ここまで見ると、データウェアハウス初心者の第一歩として/『データウェアハウスがわかる本』を読んだ
普段仕事ではデータレイク基盤の構築をメインで行っているが、そもそもデータウェアハウス(DWH)について知らない要素もあるので、その穴埋めに読んでみた。

- 作者:鈴木 健司
- 発売日: 2000/06/01
- メディア: 単行本
この本自体は2000年初版のかなり古い本にあたり、今のAWSやGCPなどのクラウドコンピューティングの要素は一切入っていない。
だけど、DWH自体の考え方は大きくぶれていないので、古いと思う要素は少なかった。
(むしろ2000年の時代からDWHを使用して機械学習しようというような要素も含まれており、20年たってもやりたいこととやれることは変わっていないんだなと思えた)
データウェアハウスというワードが仕事で急に出てきて困っているみたいな人が読むにはうってつけの書籍だと思う。
100ページ以内でさくっと読めるのもいいポイントだと思う。
目次
1章 データウェアハウスの概念2章 データウェアハウスの基本構成
3章 データウェアハウスの設計と構築
4章 多次元データウェアハウス/データマートの設計と構築
5章 データウェアハウスの活用
6章 データウェアハウス構築の開発手順
データウェアハウス(DWH)とは
基幹系データベースに蓄積されたデータをもとに、基幹系データベースとは別に構築される情報系データベース。
DataWareHouseの略がDWH。
つまり、販売戦略などの意思決定のために基幹系データベースの過去データや企業外の外部データ(経験上、OANDAなど)の情報を加工して、意思決定のために使用されるデータである。
データウェアハウスの狙いは、データから今まで知られなかった知識を得て意思決定に活用されること。
簡単に言うと雨の日は売り上げが落ちているというのは、普段気づけないが、データウェアハウスとして月単位年単位で表示するとそれが分かるようになる、ということ。
基幹系データベースをそのまま使用しない理由としては、意思決定において不要な項目があるという点や、集計軸が通常、日ベースで行われるが意思決定においては月ベースである場合がある。
そのため、そのままでは使用できないので、加工(集計や集約)してあげる必要がある。
データウェアハウスの特性
ベースとする基幹系データベースがOLTP(On-Line Transaction Processing)ということもあり、時系列データなので、データウェアハウスも時系列で集計することが多い。データウェアハウスの概念として、
・サブジェクト志向
・統合
・時系列
・普遍性
の4点が定義されている。
基幹系データベースとの違い
基幹系データベース
・定型業務処理(在庫管理や航空機の座席予約など)
・業務処理1回の受付(トランザクション)は客を待たせないようデータアクセスは最低限、高レスポンス、高スループット
・データの追加・変更・削除が可能
データウェアハウス
・意思決定支援の材料なので、定型業務は存在しない
・分析処理メインなので、大量データへのアクセス、ある程度レスポンスやスループットは低くても問題ない
・データの削除は基本的に行わない(全量洗替か差分追加(更新)となる)
サブジェクト志向
データウェアハウスの目的は上でも書いた通り企業の意思決定支援に使われるものである。例えばAmazonであなたにおすすめと商品を紹介されるケースがあるが、これは自分の購買履歴やアクセス履歴から特定されている。
snofra.hatenablog.com
これは主題(サブジェクト)が自分(顧客)であって、購買テーブルや、GoogleAnalyticsの回遊情報を組み合わせて、プロモーションしている。
これがサブジェクト指向。
基幹系データベースでいう受発注や、在庫管理などプロセスではなく、それらを使って商品や商品を利用した顧客の分析を行うこと。
統合
データウェアハウスは、色々なデータを組み合わせてテーブルとしていくが、複数社あって基幹系データベースが異なる場合はそれ毎にルールがある。例えばあるグループ会社は品目コード10桁だが、別のグループ会社は8桁など。
この各社のルールをある程度整備してデータウェアハウスとして統一した基準を作ること言う。
そこを適当にやると経験上、桁あふれでエラーになったり、割と大きい桁修正の手戻りが発生したりと面倒くさいことになる。
時系列
これはそのまま。数年単位で集計して、昨対比などを見ていくことになる。不変性
基本的に時系列データを取り扱うので、Insertがメインとなる。UpdateやDeleteは取り扱わないことで、データの恒常性を担保している。
データの世界でも現実世界と同じで過去は書き換えできないということ。
ただし、経験上データ上流側のミスなどがあるので、過去を書き換えが必要なタイミングがあるので、以下をやることが多い。
・全量削除して全件Insert(全量洗替)
→マスター系で多いやり方。上流から連携されるファイルに常に全データがある場合に多い。
・ある期間をDeleteして、その期間分Insert(差分追加)
→トランザクションデータがメイン。リカバリーを考慮。
データマートとしてのマテリアライズドビュー
データマートは上で説明していたデータウェアハウスよりも粒度の細かい部門やエンドユーザレベルに向けたデータウェアハウスになる。経験上、大きなデータウェアハウスを作って、そこから各部門ごとへデータマートを切り出していることがあった。
その際のデータマートはビューであった。
この書籍でもデータマートはビュー、マテリアライズドビューであると説明されている。
マテリアライズドビューとは
データベース管理システムは関係モデルに従うため、ビュー は仮想的な テーブル であり、データベースに対するクエリの結果を表す。ビューを参照または更新すると、その処理はビューの対象となった実際のテーブルへの参照または更新へ変換され、実行される。
マテリアライズドビュー (Materialized View; 体現ビューともいう)はこれとは異なるアプローチを取り、クエリの結果を実際のテーブルにキャッシュする。キャッシュされたデータは元のテーブルが変更されるたびに更新される。そのため、最新でない状態を取得する可能性はあるが、効率的なアクセスが可能になる。特にデータウェアハウスでは実際のテーブルに対して頻繁にクエリを実行することは非常にコストが高いため、マテリアライズドビューが有効である。
マテリアライズドビュー - Wikipedia
ビューはアクセスしたときにinputのテーブルから情報を抽出してくるが、マテリアライズドビューはデータをキャッシュしておける。
分析を行た目に結合や集計などが行われているため、パフォーマンス懸念があった。そのため、マテリアライズドビューを使用してあらかじめ実行結果を格納しておくことによりパフォーマンス問題を解決できる。
Redshiftでは2020/03/12現在、プレビュー中だが今後使用可能になるよう。
データマート構築した際もビューでパフォーマンス懸念があったので、マテリアライズドビューが使えるようになると楽だなーと。
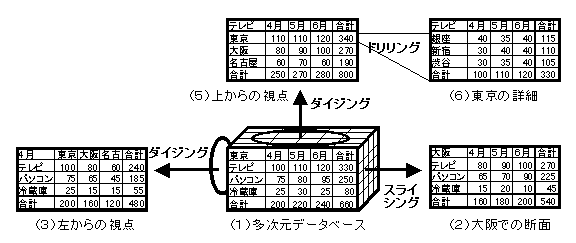
多次元データモデル
これを見るのが分かりやすい。www.atmarkit.co.jp
多次元データモデルは、販売戦略などの意思決定のためのデータとしてどのようなデータが必要なのか、という点において活用される。
ここからわかるように、データマートで部門ユーザが分析したい軸はたくさんあるし、粒度もそれぞれ違う。
このような要約や詳細など多次元的にみられるデータを指す。
スタースキーマ
多次元データベースで分析したいデータの粗さは定めることはできるが、実際は売上なら、売上テーブルを中心に、商品情報があるテーブルや、購入したユーザ情報テーブルなどデータが存在しており、それらと紐づいてようやく販売戦略などの意思決定のためのデータとなりえる。イメージとしては以下となる。
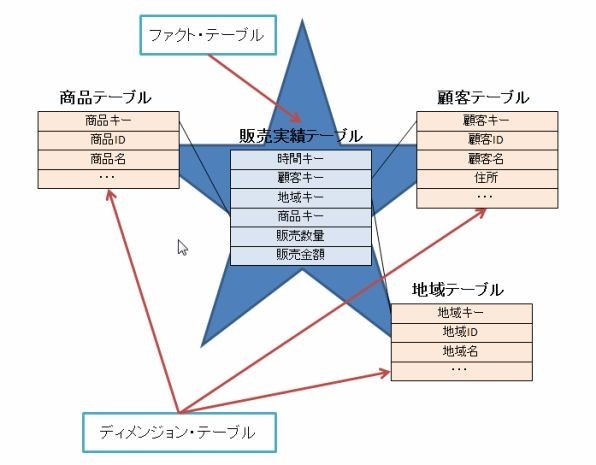 *2
*2
このような構造をスタースキーマと呼ぶ。
またその中心(売上テーブル)をファクトテーブル(事実表)、そのファクトテーブルを修飾するテーブルをディメンションテーブル(次元表)と呼ぶ。
データマートを構築するときに最後TableauなどBIツールを使用して可視化することになる。
経験上、そのデータマートのビューの結合の際にこのスタースキーマを考えることが多かったように思える。
基幹系データベース
基幹系データベースは受注や発注、在庫管理、経理などのメイン処理を行っているデータとなる。業態や組織の構成、システム化の度合いなどによりどのようなシステムが該当するかは異なるが、止まると業務自体がストップしてしまったり、事業に深刻な影響が及ぶようなものをこのように呼ぶ。
e-words.jp